The Unforgeable Seal: Understanding ECDSA Digital Signatures

Ever wondered how Bitcoin and Ethereum verify that YOU actually sent a transaction? The answer is ECDSA (Elliptic Curve Digital Signature Algorithm) - a clever mathematical system that proves you authorized a message without revealing your secret password.

The Problem We're Solving

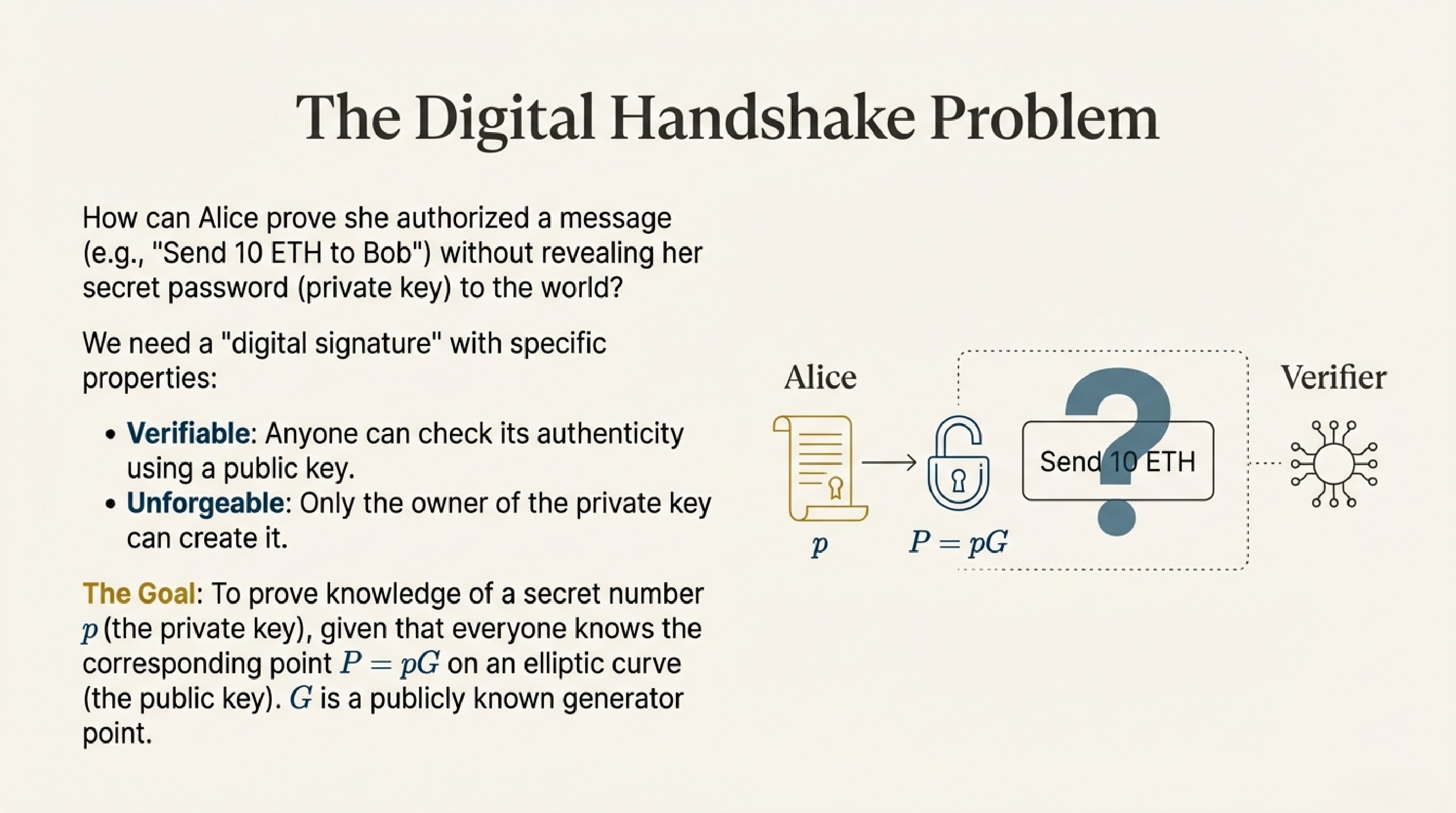
Imagine Alice wants to send a message: "Send 10 ETH to Bob"

She needs to prove two things:

1. She really sent it (anyone can verify)
2. Nobody can fake her signature (only she can create it)

But here's the catch: she can't reveal her private key (secret password) to prove it, or everyone could steal her money!

The Magic Behind It: One-Way Math

ECDSA works because of a mathematical "trapdoor" - something easy to do one way but nearly impossible to reverse.

Think of it like mixing paint:

• Easy: Mix blue + yellow → get green ✅
• Impossible: Look at green paint → figure out exact amounts of blue and yellow ❌

In ECDSA terms:

• Easy: Private key × Generator Point → Public key ✅
• Impossible: Public key → Find the private key ❌

This is called the Elliptic Curve Discrete Logarithm Problem - it's so hard that even supercomputers can't solve it in a reasonable time.

How ECDSA Works

Creating a Signature (Signing)

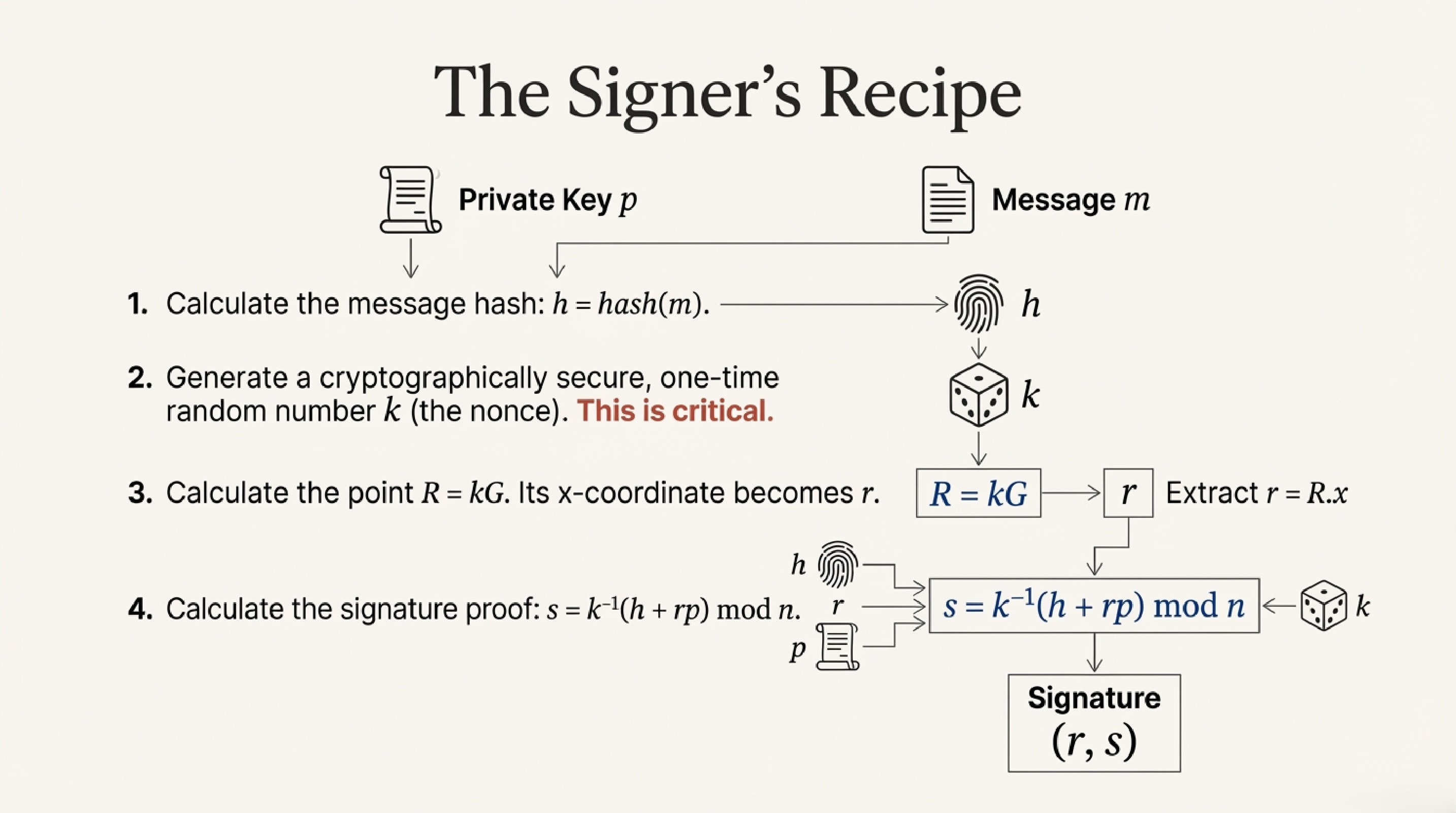
When Alice signs a message, here's what happens:

1. Hash the message - Turn "Send 10 ETH to Bob" into a fixed-size number
2. Pick a random number (k) - This is super important and must NEVER be reused!
3. Do some math - Create two numbers called r and s
4. Send the signature - The pair (r, s) is the signature

The magic is in step 3: the formula s = k⁻¹(hash + r × private_key) ties together the message, the private key, and the random number in a way that can be verified but not forged.

Checking a Signature (Verification)

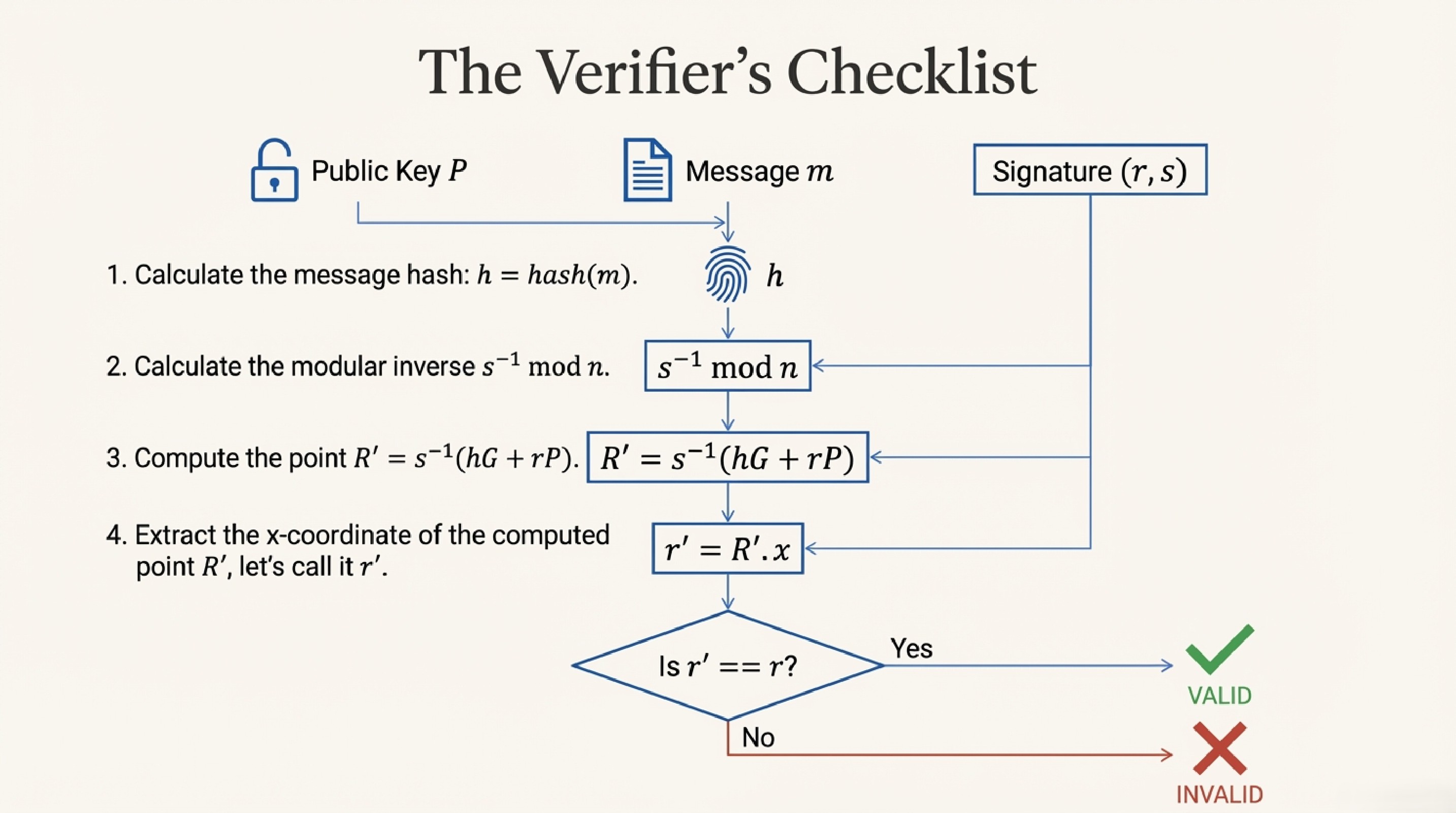
When someone wants to verify Alice's signature:

1. Hash the message - Get the same number Alice got
2. Do some calculations - Use the public key and signature
3. Check if it matches - If the math works out, the signature is valid!

The verifier never sees Alice's private key, but the math proves she must have known it to create the signature.

Why This Is Secure

ECDSA is secure because of three key principles:

The One-Way Function: You can't work backwards from the public key to find the private key. It's mathematically protected.

The Random Challenge: The signature includes information that couldn't be pre-computed. An attacker can't prepare a fake signature in advance.

Circular Dependency: The signature formula creates a chicken-and-egg problem for attackers - they'd need to know the answer before they can start calculating, which is impossible.

The Critical Warning: Never Reuse the Random Number

Here's where things get dangerous. Remember that random number k from the signing process? If you ever use the same k for two different messages, your private key can be calculated!

Real disasters from reusing k:

Sony PS3 Hack (2010): Sony's developers used the same k for all PlayStation 3 firmware signatures. Hackers figured this out, extracted Sony's private key, and could sign their own code. The PS3 security was completely broken.

Bitcoin Thefts: Multiple Bitcoin wallets had weak random number generators that sometimes produced the same k value. Attackers detected these repeated values and stole users' Bitcoin by recovering their private keys.

The lesson: k must be truly random, kept secret, and never ever reused.

Why ECDSA Matters

ECDSA is everywhere in blockchain and crypto:

Bitcoin & Ethereum: Every transaction you send is signed with ECDSA

Cryptocurrency Wallets: Your wallet uses ECDSA to prove you own your coins

Smart Contracts: Signatures authorize contract interactions

Web Security: Many HTTPS certificates use ECDSA

The beauty of ECDSA is its efficiency. A 256-bit ECDSA key provides the same security as a 3072-bit RSA key - that's 12 times more efficient!

What Makes a Good Digital Signature?

Think of ECDSA like a high-tech wax seal on an envelope:

• Anyone can verify ✅ it's your seal (using your public key)
• Only you can create ✅ it (requires your private key)
• Can't be copied ✅ to another message (tied to the content)
• Can't be forged ✅ (protected by hard math problems)

The Future: Post-Quantum Signatures

ECDSA has one weakness: quantum computers. While today's computers can't break ECDSA, future quantum computers theoretically could.

Researchers are already preparing alternatives:

• CRYSTALS-Dilithium (lattice-based)
• SPHINCS+ (hash-based)
• Rainbow (multivariate)

These "post-quantum" signature schemes will protect us when quantum computers become powerful enough to threaten ECDSA.