How Merkle Trees Secure Blockchain and Beyond

Ever wondered how Bitcoin can verify thousands of transactions in a single block without checking each one individually? Or how Git knows exactly which files changed in your repository? The answer is the Merkle tree - an elegant data structure that lets you verify massive amounts of data by checking just a tiny piece of it.

The Problem We're Solving

Imagine you're downloading a file with 1 million transactions from an untrusted source. You need to verify that:

Nothing was tampered with (data integrity)
A specific transaction is included (membership proof)
You can do this efficiently (without checking all 1 million items)

Traditional approach? Hash all 1 million transactions together. But there's a problem: if you want to verify just ONE transaction, you'd need to download ALL of them first!

This is where Merkle trees shine.

What Is a Merkle Tree?

A Merkle tree is a binary tree where:

Leaf nodes contain hashes of actual data (transactions, files, etc.)
Parent nodes contain hashes of their children combined
Root node (Merkle root) represents the hash of the entire dataset

Think of it as a pyramid of trust that collapses all your data into a single fingerprint.

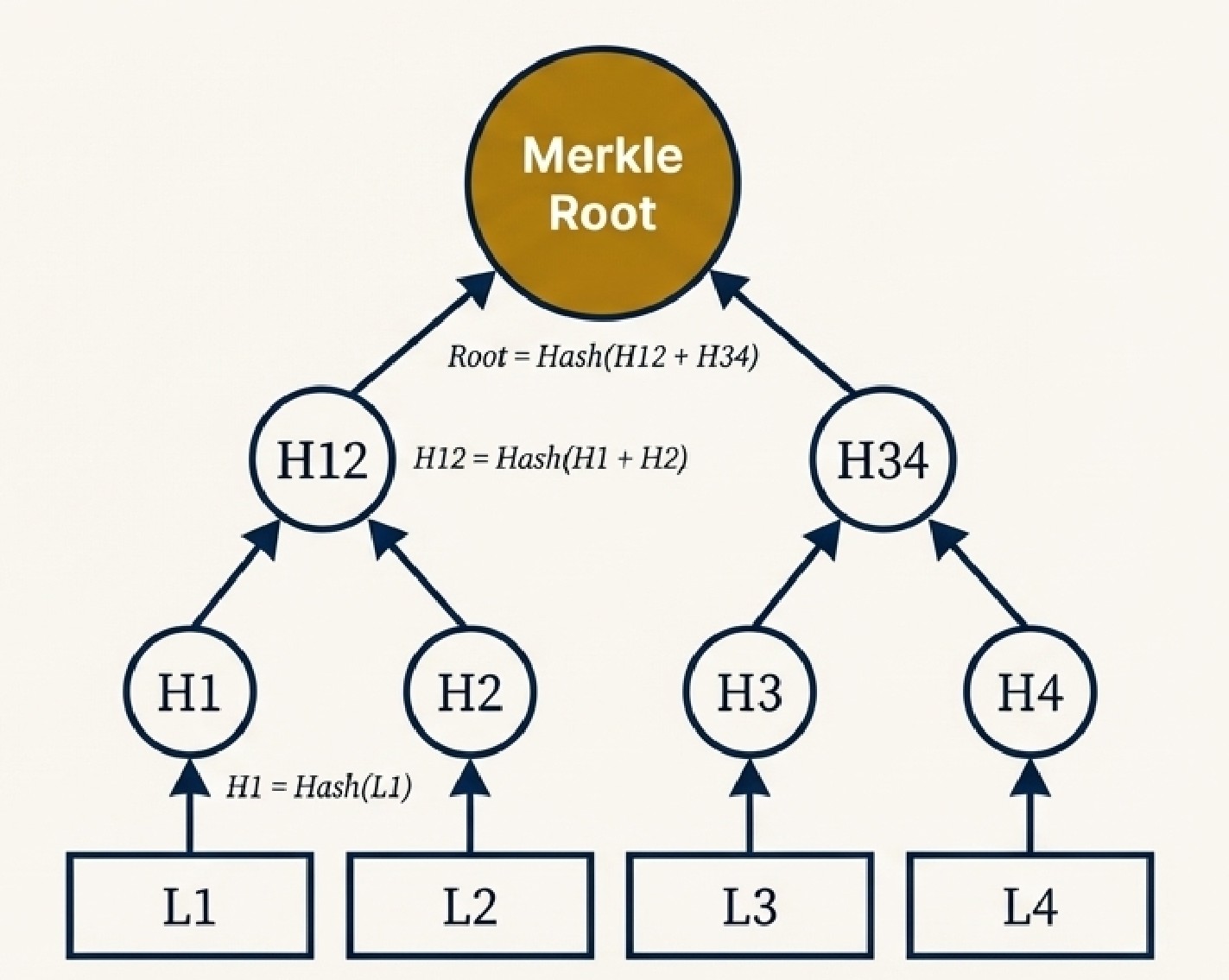
Merkle Tree

The tree builds from bottom to top:

Hash each Leaf node individually
Combine adjacent hashes and hash them again
Repeat until you reach a single root hash

How Merkle Proofs Work

Here's the magic: to prove L1 is included, you don't need all leaves. You only need:

Hash(L1) - the leaf itself
H2 - the hash of L2
H34 - the hash of L3 and L4

With these 3 hashes, anyone can verify L1 is in the tree by:

Computing Hash(L1H2) = Hash(Hash(L1) + Hash(H2))
Computing Root = Hash(Hash(L1H2) + Hash(H34))
Comparing with the known root

Result: You verified 1 out of 4 transactions using only 3 hashes instead of 4. Now scale this to 1 million transactions: you'd need only ~20 hashes instead of 1 million!

Real-World Applications

1. Bitcoin Block Verification

Every Bitcoin block contains a Merkle root in its header. This enables:

Light clients (SPV wallets) to verify transactions without downloading the entire blockchain
Proof of inclusion for any transaction with just a few hashes (~10-15 for typical blocks)

Example: Your mobile Bitcoin wallet doesn't store 500GB+ of blockchain data. It only stores block headers (~80MB) and uses Merkle proofs to verify your transactions.

2. Ethereum State Verification

Ethereum uses a more complex variant called a Merkle Patricia Tree to store:

Account balances
Smart contract code
Contract storage

This allows:

Stateless clients to verify specific account states
Light clients to check balances without full node data
Efficient state proofs for Layer 2 solutions

3. Git Version Control

When you git commit, Git creates a Merkle tree of your files:

Each file is hashed (blob)
Directory structures are hashed (tree)
The commit itself contains the root hash

Benefits:

Instant change detection: different root = something changed
Tamper-proof history: changing any file changes the entire commit hash
Efficient diff operations: only changed branches need rehashing

4. IPFS (InterPlanetary File System)

IPFS uses Merkle DAGs (Directed Acyclic Graphs) to:

Address content by hash (content addressing)
Deduplicate identical files across the network
Verify file integrity on download
Enable efficient partial downloads

5. Certificate Transparency Logs

Major browsers use Merkle trees to verify SSL certificates:

All issued certificates are logged in public Merkle trees
Browsers can verify a certificate is properly logged
Detects misissued or fraudulent certificates
Append-only logs prevent tampering

Why Merkle Trees Are So Powerful

Efficiency

For N data items, verification requires only O(log N)hashes:

1,000 items → ~10 hashes
1,000,000 items → ~20 hashes
1,000,000,000 items → ~30 hashes

Security

Changing any leaf cascades up:

Altering L1 changes Hash(L1)
Which changes Hash(L1H2)
Which changes the Root
The tampered root won't match the trusted root

Scalability

Merkle proofs enable:

Light clients (verify without full data)
Sharding (verify cross-shard transactions)
Layer 2 solutions (commit batches efficiently)

Simple Implementation Example

Here's how you might build a basic Merkle tree in pseudocode:

function buildMerkleTree(transactions):
    // Start with leaf nodes
    nodes = [hash(tx) for tx in transactions]
    
    // Build tree bottom-up
    while len(nodes) > 1:
        newLevel = []
        for i in range(0, len(nodes), 2):
            left = nodes[i]
            right = nodes[i+1] if i+1 < len(nodes) else left
            parent = hash(left + right)
            newLevel.append(parent)
        nodes = newLevel
    
    return nodes[0]  // Merkle root

function verifyProof(leaf, proof, root):
    current = leaf
    for sibling in proof:
        current = hash(current + sibling)
    return current == root

Conclusion

Merkle trees are the unsung heroes of modern distributed systems. They transform the problem of verifying large datasets from "download everything and check" to "download a tiny proof and verify instantly."

Every time you:

Send a Bitcoin transaction from your phone
Use a light Ethereum wallet
Push code to GitHub
Download from IPFS

You're leveraging the power of Merkle trees. They're proof that elegant mathematics can solve real-world problems at scale.

However, Merkle trees are not a silver bullet. You must trust the Merkle root comes from a reliable source, and they don't protect against withholding attacks where valid data is hidden. For efficient updates, additional structures like Merkle Patricia Trees are required. Tree balance also matters because unbalanced trees reduce efficiency. Most implementations use padding for incomplete levels to maintain balance.